Cette présentation essaie d’être à la fois rigoureuse et simple. Si vous n’êtes pas familier avec les équations, ne vous laissez pas impressionner, lisez seulement les textes. Pour ceux qui maîtrisent les concepts mathématiques utilisés ici, désolé d’être peut-être un peu trop didactique.
Cet exposé nécessite la compréhension de ce qu’est une option. Dans toute la suite nous nous placerons dans le cas d’un call.
Notations
St : cours de l’actif sous jacent à l’instant t
r : taux d’intérêt sans risque
s t : volatilité à l’instant t
K : prix d’exercice
t : date actuelle
T : date de l’exercice
G : prix du call (prime)
Formule de Black et Scholes
L’hypothèse de base est que les variations du cours du sous-jacent ont deux causes de variation :
Cela donne :
![]()
Un mouvement brownien est une fonction aléatoire telle que :
En clair, il s’agit d’une fonction aléatoire dont l’évolution future ne dépend pas de l’évolution passée.
Dans le modèle de Black et Scholes classique les paramètres r, m et s sont supposés constants, mais le raisonnement reste valable si ces paramètres sont des fonctions dépendant du temps
Ces hypothèses conduisent à la formule de Black et Sholes :

où N désigne la fonction de répartition de la loi normale et ln le logarithme népérien
Lorsque les coefficients r et s dépendent du temps, les mêmes formules restent valables à condition de remplacer s 2 et r par :

De ces formules, on obtient les expressions des " lettres grecques " :
![]()
![]()
![]()
![]()
Les hypothèses du modèle
Amélioration du modèle
Comme nous venons de le voir, nous évaluons la volatilité de manière implicite. Nous considérons donc que entre l’instant t et l’instant T, l’actif sous-jacent aura la même volatilité (celle de l’instant t). Ce n’est évidemment pas ce que suggère notre expérience.
Nous utilisons par ailleurs dans le modèle de Black et Scholes l’hypothèse selon laquelle les variations des cours des sous-jacents sont distribués de façon normale (c’est-à-dire suivant une gaussienne). L’expérience montre que ce n’est pas tout à fait vrai et que l’utilisation de loi dont les queues de distribution sont plus épaisses est plus appropriée.
Nous allons donc essayer d’introduire une fonction de volatilité, s u, dépendant du temps. Il s’agit de prévoir à l’instant t l’évolution de la volatilité jusqu‘au temps T. Pour cela nous allons utiliser les modèles hétéroscédastiques ARCH-GARCH.
Nous allons limiter l’exposé au modèle GARCH(1,1) qui se révèle d’expérience le plus efficace.
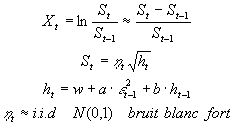
Nous essayons donc de modéliser les variations relatives Xt du cours du sous-jacent St. Ces variations relatives sont considérées comme un bruit blanc, c’est-à-dire des variables aléatoires de moyenne nulle et non corrélées entre elles, mais d’écart-type variable. Tout l’enjeu de la modélisation consiste à trouver les bons paramètres a, b et w permettant une bonne modélisation.
Une fois ces paramètres trouvés, il reste à reprendre le raisonnement de Black et Scholes afin d’aboutir à un résultat similaire. Toutefois, dans ce cas il n’existe plus de formules explicites pour évaluer le prix de l’option, mais seulement des méthodes numériques.